A Time-to-Compromise Model of IDS Alerts and Login Attempts
System Model
Let \(s_t = [x_t, y_t, t]\) be the state at time \(t\) where \(x_t\) is the number of IDS alerts at time \(t\) and \(y_t\) is the number of failed login attempts at time \(t\).
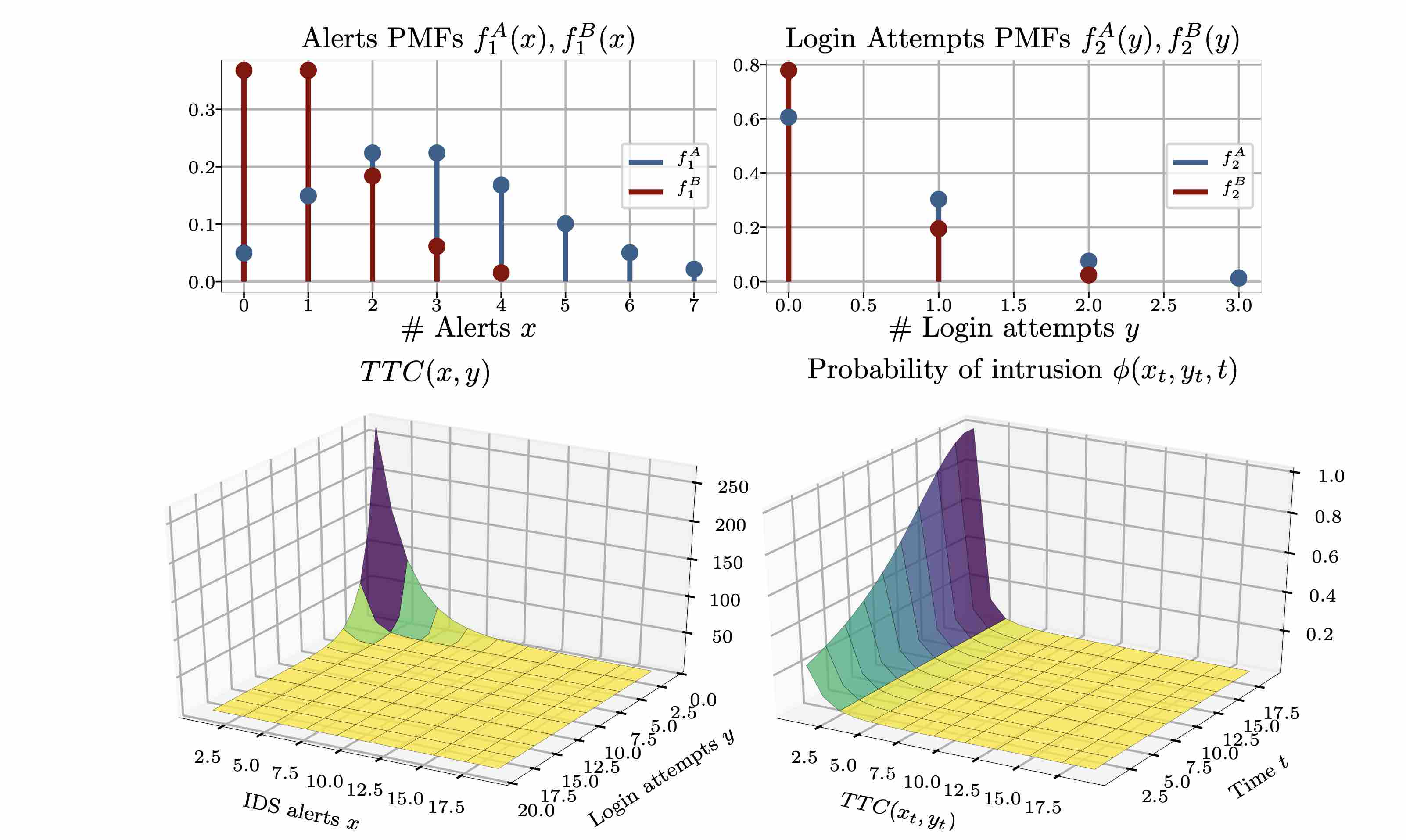
We assume that the distribution of alerts and the distribution of the number of failed login attempts are different when there is a network intrusion in progress compared to when there is no intrusion in progress. Let \(f_1^A, f_2^A\) be the probability distributions of alerts and failed login attempts when no intrusion is in progress and let \(f_1^B, f_2^B\) be the distributions when no intrusion is in progress. Further, let \(\phi([x_t, y_t, t])\) be the probability that an intrusion is in progress in state \(s_t = [x_t, y_t, t]\).
A Review of Time-to-Compromise
The time-to-compromise (TTC), is a metric used to assess the risk that an infrastructure is compromised [1][2]. Specifically, the TTC metric takes as input various parameters of the infrastructure, such as the number of vulnerabilities and the estimated time it takes to develop a new exploit, and outputs an expected time until the infrastructure is compromised. For our purposes, TTC is a natural metric for defining the probability of an intrusion \(\phi(x, y, t)\), where the probability of an intrusion is decreasing in the TTC.
A TTC Model of IDS Alerts and Login Attempts
We consider a model where the IDS alerts and failed logins are Poisson-distributed and where the expected number of alerts and failed logins is larger when an intrusion is in progress compared to when no intrusion is in progress (e.g. \(\mathbb{E}_{X \sim f_1^{A}}[X] > \mathbb{E}_{X \sim f_1^{B}}[X]\)). Further, to define the probabiliy of an intrusion given the number of IDS alerts and login attempts, we use the time-to-compromise (TTC) metric.
\(f_1^{A} \sim Pois(\lambda^A_1=3), f_2^{A} \sim Pois(\lambda^A_2=0.5)\) \(f_1^{B} \sim Pois(\lambda^B_1=1), f_2^{B} \sim Pois(\lambda^B_2=0.25)\) \(\phi(x, y, t) \triangleq \frac{1}{0.99ttc^{3} + 0.01(T-t)^{2}}\)
As the only parameters available are the number of IDS alerts and the number of failed logins, we redefine the TTC models from [1][2] in terms of those two parameters:
\[\xi(x,x_{max}) \triangleq \frac{x}{x_{max}}\left(1 + \sum_{t=2}^{floor(s(1-\frac{x}{x_{max}}))}\left[t\prod_{i=2}^t\left(\frac{x(1-\frac{x}{x_{max}}-i + 2)}{x_{max}-i+1}\right)\right]\right)\] \[s \triangleq \frac{y}{y_{max}}, m(s) \triangleq 83\cdot 3.5^{4*s-2.7}-82\] \[f(s) \triangleq 0.145\cdot 2.6(2s + 0.007)-0.1\] \[P_1 \triangleq 1 - e^{-x\frac{m(s)}{k}}\] \[u \triangleq (1-f(s))^{x}\] \[t_1 \triangleq 5.8E(x,s)\] \[t_2\triangleq (\frac{1}{f(s)}-0.5)32.42 + 5.8\] \[E(x,y) \triangleq \xi(floor(f(s)x), s)(ceil(f(s)s)-f(s)x) + \xi(ceil(f(s)s),x)(1-ceil(f(s)x)+f(s)x)\] \[TTC(x,y,x_{max}) \triangleq P_1 + t_1(1-P_1)(1-u) + t_2u(1-P_1)\]where \(x \in [0, x_{max}]\) is the number of alerts and \(y \in [0, y_{max}]\) is the number of failed logins.
The resulting distriubtions looks as follows:
References
-
[1] Time-to-Compromise Model for Cyber Risk Reduction Estimation. McQueen, Miles A and Boyer, Wayne F. and Flynn, Mark A. and Beitel, George A. Quality of Protection, Springer US, Boston, MA
-
[2] The \(\beta\)-Time-to-Compromise Metric for Practical Cyber Security Risk Estimation. Zieger, Andrej and Freiling, Felix and Kossakowski, Klaus-Peter. 2018 11th International Conference on IT Security Incident Management IT Forensics (IMF).