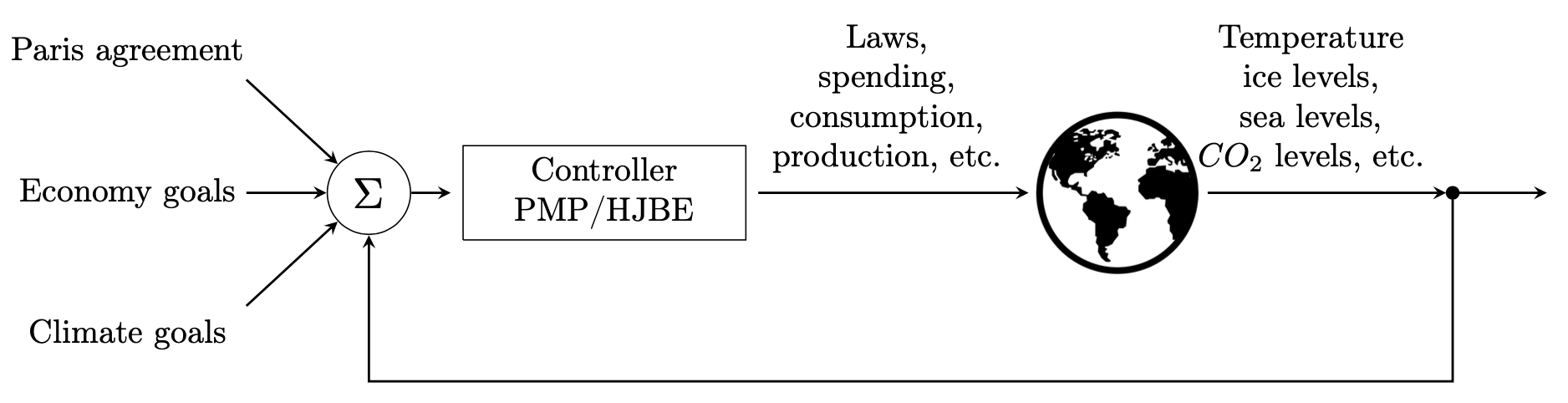
Optimal Control for Climate Manipulation
The global climate is changing. Since the end of the 19th century, the global average temperature has increased with 1 degree and the expectation is that it will increase by an additional 2-6 degrees by the end of the 21st century unless drastic measures are taken [12,11]. One of the main causes of the global warming is believed to be the increased levels of greenhouse gases in the atmosphere, which was hypothesized by Fourier already in 1807 [4,3]. This “greenhouse effect” keeps the Earth’s temperature far higher than it would otherwise be. As a response, climate engineering has been suggested. Climate engineering seeks to reduce global warming by manipulating the climate; for example via reducing the emission of greenhouse gases. In 2015, a legally binding international treaty, known as the Paris Agreement, was adopted by \(193\) states [7,10]. This treaty declares that global warming should be kept well below \(2\) degrees compared to pre-industrialization (mid 19th century) levels, which requires significant climate engineering efforts. In this blog post, I show how the theory of optimal control can guide climate engineering to achieve desired effects on the climate and meet the Paris agreement. I model the global climate as a nonlinear dynamical system, derive structural properties of the optimal control strategy using Pontryagin’s minimum principle, and I compute the numerical control values using nonlinear constrained optimization.
Climate System Model
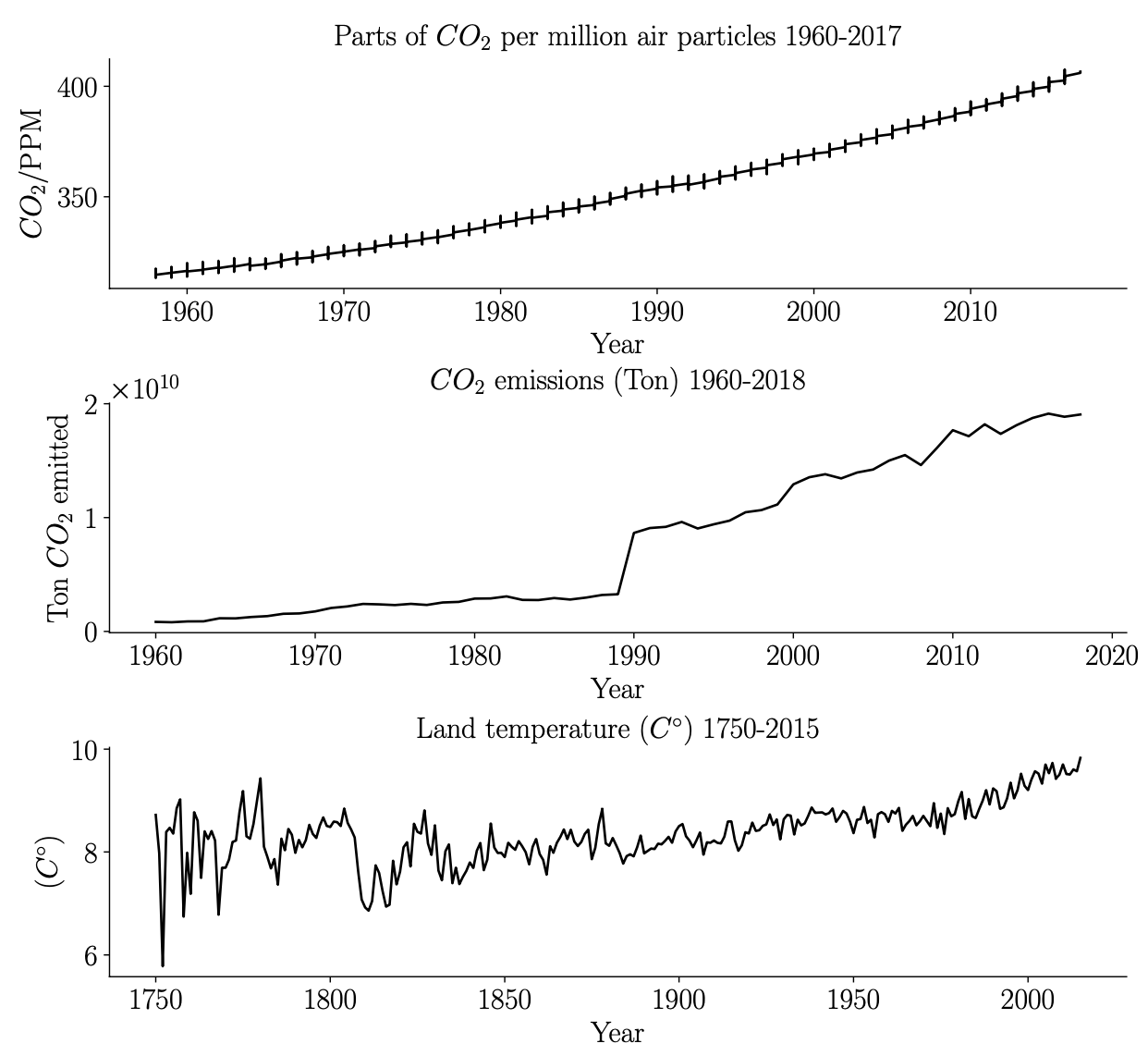
Our model of the climate system is focused on global warming and is inspired by the models in [8] and [5]. The purpose of the model is to capture the relationships between CO2 emissions, Earth’s temperature, and the concentration level of CO2 in the atmosphere. Historical data of these relationships are shown in Fig. 2. The data is obtained from [1] and additional post processing of the data was provided via [2].
Accurate modeling of the climate is difficult as it depends on all the natural spheres (e.g. atmosphere, biosphere, hydrosphere, and geosphere). For our purposes, analytic tractability is valued higher than exact precision. We therefore choose to use a model with few parameters to ensure computational tractability and to obtain theoretical insight. In particular, we use a nonlinear dynamical system model of two states and one control input (see below).
States. The state is \(x(t)=\begin{bmatrix}x_1(t) & x_2(t) \end{bmatrix}^T \in \mathbb{R}^2\) where \(x_1(t)\) is the atmospheric concentration of \(CO_2\) and \(x_2(t)\) is the global temperature (\(C^{\circ}\)) increase over preindustrial level (mid 19th century level).
Controls. The climate system takes one control input: the amount of \(CO_2\) emissions at time \(t\) (unit: billions of tons of \(CO_2\)), i.e \(u(t) \in \mathbb{R}_{+}\).
Dynamics. Global warming is assumed to evolve dynamically as a function of the atmospheric concentration of \(CO_2\) and the current temperature, and to be described by the following relationships:
\(\dot{x}_1(t) = f_1(x_1(t), x_2(t), u(t))=\alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t)\) \(\dot{x}_2(t) = f_2(x_1(t), x_2(t))=\delta(\epsilon x_2(t) - x_1(t))\) \(f(x(t), u(t))\triangleq \begin{bmatrix} f_1(x_1(t), x_2(t), u(t)) \\ f_2(x_1(t), x_2(t)) \end{bmatrix}\)
where \(\alpha, \beta, \gamma, \delta\), and \(\epsilon\) are constants. Here, \(\delta\) represents the time delay of temperature changes in response to increased \(CO_2\) emissions per year, \(\alpha \in (0,1]\) is the fraction of \(CO_2\) emissions that enter the atmosphere, \(\beta \in [0,1]\) is the rate of removal of \(CO_2\) from the atmosphere (per year), \(\gamma \geq 0\) indicates how much the \(CO_2\) concentration in the atmosphere decays in relation to the temperature increase level, and \(\epsilon \geq 0\) is the increase in global mean temperature in response to increasing \(CO_2\) equivalent concentration.\newline
The first state equation states that the atmospheric concentration of \(CO_2\) (\(x_1(t)\)) grows with the amount of new emissions of \(CO_2\) (\(u(t)\)) and declines through environmental absorption at a rate that depends on the global temperature increase \(x_2(t)\). The second state equation indicates that global temperature (\(x_2(t)\)) adjusts gradually, at a rate \(\delta > 0\), to an equilibrium level that depends on the concentration of \(CO_2\) in the atmosphere (\(x_1(t)\)).
End time. We consider a fixed end time \(t_f\).
Control constraints. The control is bounded below: \(u(t) \geq 0\) \(\forall t \in [0,t_f]\).
Initial state. The initial state is given by measuring the current temperature increase and the current concentration of \(CO_2\).
Time dependence. The dynamical system is time-invariant in the sense that it does not depend on time explicitly, only implicitly through \(x(t)\) and \(u(t)\).
System identification
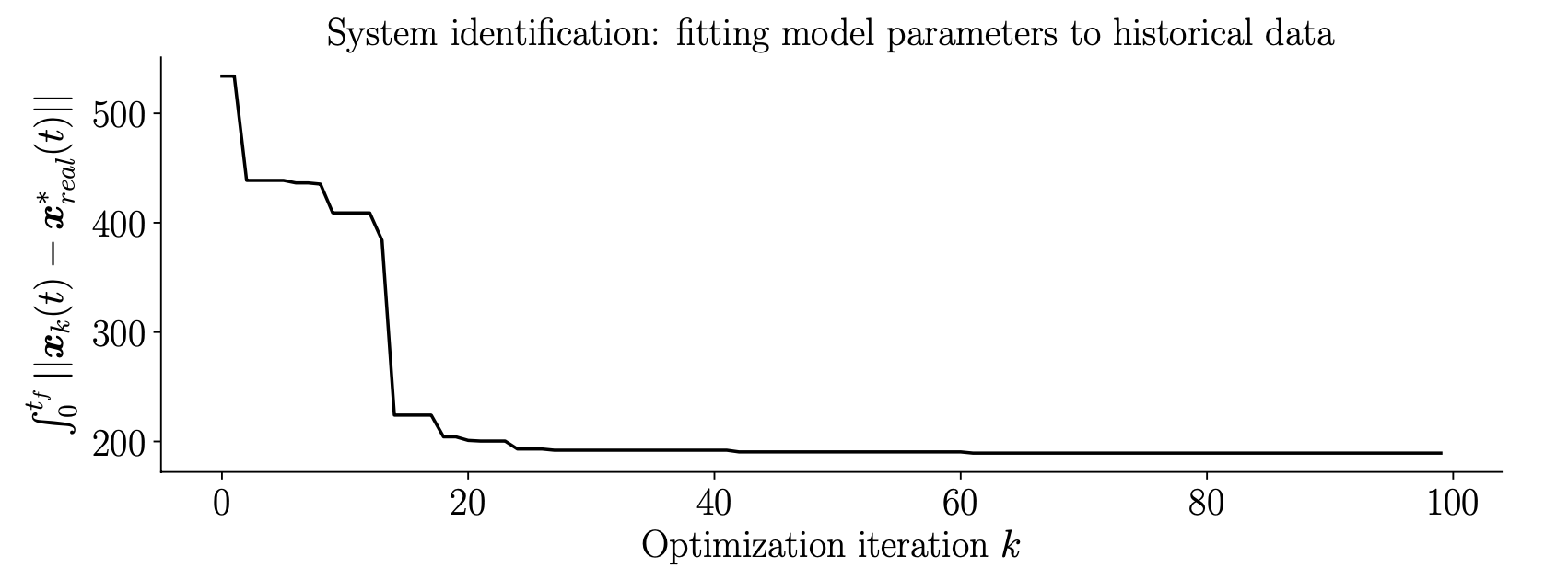
The system model includes five free parameters: \(\alpha, \beta, \gamma, \delta, \epsilon\). We estimate these parameters based on historical climate data (see the figure above). Specifically, we use Bayesian optimization [6] to find model parameters that minimize the difference between the model’s predictions and historical climate data from the years \(1960-2015\). Formally, we minimize the optimization criterion:
\[\min_{\alpha, \beta, \gamma, \delta, \epsilon} \int_{t_i}^{t_f}||x(t) - x_{real}(t)||dt \\ \quad \quad \text{subject to }\\ t_f=2015\\ t_i =1960\\ x(1960)=x_{real}(1960)\\ \dot{x}(t)=f(x(t), u(t)) \quad t\in [t_i,t_f]\\ u(t) = u_{real}(t) \quad t \in [t_i,t_f]\]where \(x(t)\) is the predicted values of \(CO_2\) concentration and temperature increase when \(u_{real}(t), t \in [t_i,t_f]\) is input to the model and \(u_{real}(t)\) and \(x_{real}(t)\) refers to the actual \(CO_2\) emissions, the actual \(CO_2\) levels in the atmosphere, and the actual temperature increase recorded at year \(t\), where \(t \in [1960,2015]\).
The convergence curve of Bayesian optimization is shown below:
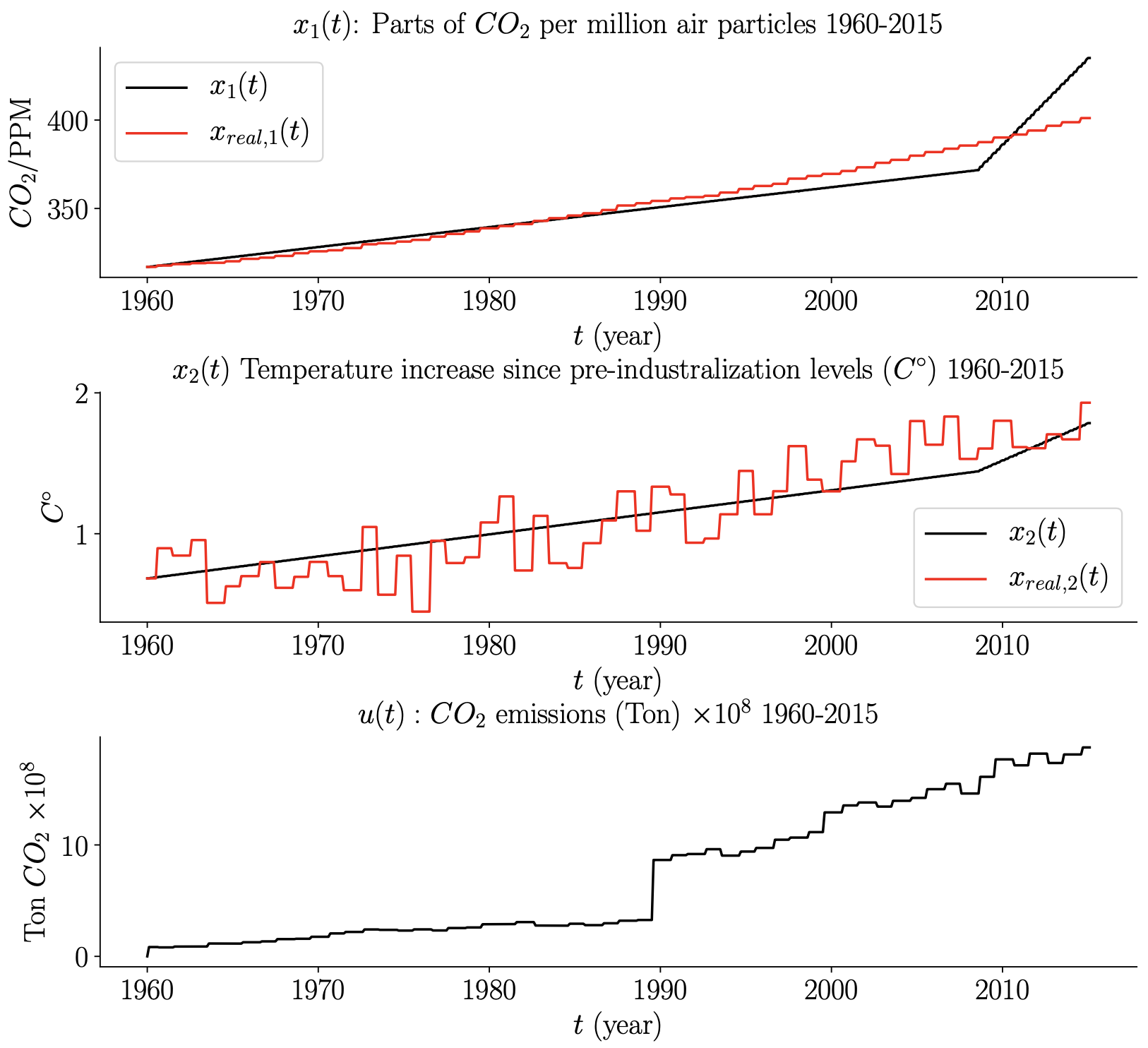
A comparison between the state trajectory predicted by the model with the optimized parameters \(\alpha=0.93,\delta=-0.05,\beta=0.01,\gamma=3.398,\epsilon=0.14\) and the historical climate data is shown below:
The Optimal Control Problem
The goal is to find a control law for climate engineering that minimizes global warming over the coming thousand years (the years \(2000-3000\)) at the minimal cost (reducing \(CO_2\) emissions involves a cost). We express this objective mathematically as follows:
\[\min_{u(\cdot)} J(x(\cdot), u(\cdot)) = \min_{u(\cdot)} \left[\int_{0}^{t_f} \left(x_2(t)-\ln(u(t)) \right)dt\right] \\ \quad\quad \text{subject to }\\ \dot{x}(t) = f(x(t), u(t)) \quad t \in [0,t_f]\\ t_f=100\\ u(t) \geq 0\\ x(0) = x_{real}(2000)\]where we have normalized the time interval to start from \(t=0\) rather than \(t=2000\).
The dynamics are: \(\dot{x}(t) = f(x(t), u(t))= \begin{bmatrix} f_1(x_1(t), x_2(t), u(t)) \\ f_2(x_1(t), x_2(t)) \end{bmatrix} = \begin{bmatrix} \alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t) \\ \delta(\epsilon x_2(t) - x_1(t)) \end{bmatrix}\)
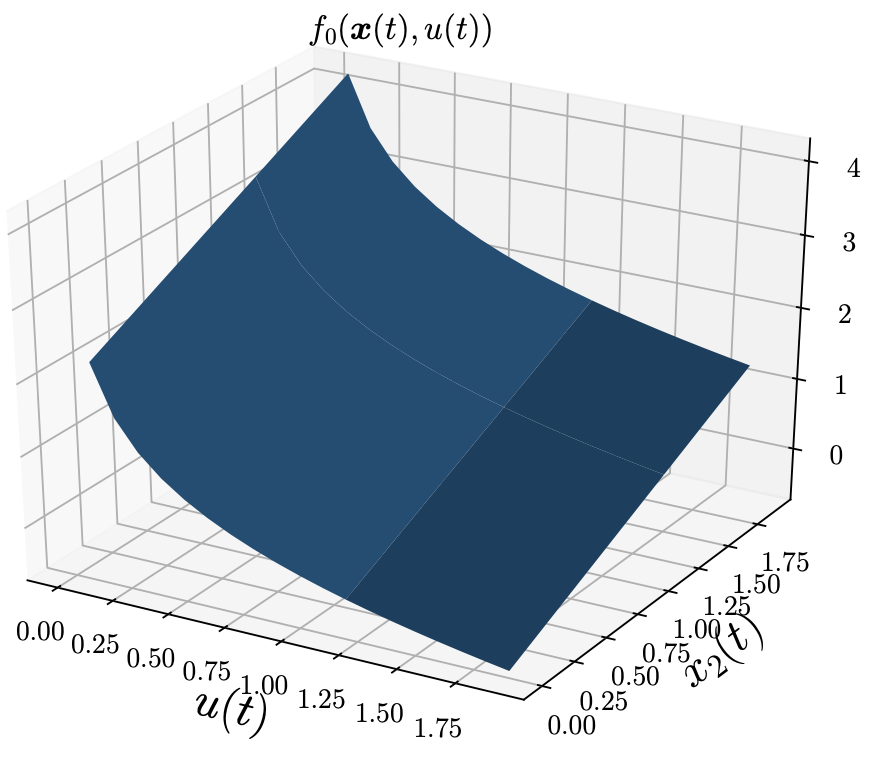
and the stage cost (see the figure below): \(f_0(x(t), u(t)) \triangleq x_2(t)-\ln(u(t))\)
is a convex function that is linearly increasing in the temperature \(x_2(t)\) and decreasing in the amount of \(CO_2\) emissions (assuming that social welfare benefits from increased production).
Analysis of the Optimal Controller using Pontryagin’s Principle
To analyze the structural properties of the optimal control law of the control problem we apply the necessary optimality conditions of Pontryagin’s principle [9].
The Hamiltonian \(H(t,x(t), u(t), \lambda(t))\) of is: \(H(x(t), u(t), \lambda(t)) = f_0(x(t), u(t)) + \lambda^T(t)f(x(t), u(t))\\ = x_2(t)-\ln(u(t)) + \lambda_1(t)\left(\alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t)\right) + \lambda_2(t)\left(\delta(\epsilon x_2(t) - x_1(t))\right)\) where \(\lambda(t) \in \mathbb{R}^{2}\) is the adjoint vector that adjoins the dynamics constraint with the stage cost and satisfies the adjoint equations: \(\dot{\lambda}_1(t) = -\frac{\partial H(x(t), u(t), \lambda(t))}{\partial x_1}\\ \dot{\lambda}_2(t) = -\frac{\partial H(x(t), u(t), \lambda(t))}{\partial x_2}\) subject to the boundary conditions: \(\lambda_1(t_f) = \frac{\partial \phi(x(t))}{\partial x_1} = 0\\ \lambda_2(t_f) = \frac{\partial \phi(x(t))}{\partial x_2} = 0\)
Given the adjoint vector and the Hamiltonian defined as above, Pontryagin’s principle maps the optimality condition \(J(x^{*}(\cdot), u^{*}(\cdot)) \leq J(x(\cdot), u(\cdot))\) \(\forall x(\cdot),u(\cdot)\) in the primal space to the following condition in the dual space: \(H^{*}(x^{*}(\cdot), u^{*}(\cdot), \lambda(t)) = \min_{u(\cdot)}H(x^{*}(\cdot), u(\cdot), \lambda(t)) \quad\quad \forall t \in [t_i,t_f]\) In our case, the above conditions implies that: \(u^{*}(t) = \tilde{\mu}(t,x(t), u(t)) \triangleq arg\min_{u(t)}\left[x_2(t)-\ln(u(t)) + \lambda_1(t)\left(\alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t)\right) + \lambda_2(t)\left(\delta(\epsilon x_2(t) - x_1(t))\right)\right]\\ =arg\min_{u(t)}\left[\underbrace{-\ln(u(t)) + \lambda_1(t)\alpha u(t)}_{\text{convex in $u$}} \right]\) Since the expression inside the minimization is convex in \(u\), a necessary and sufficient condition for minimality is: \(n 0 = \frac{\partial}{\partial u}\left(-\ln(u(t)) + \lambda_1(t)\alpha u(t)\right) = \lambda_1(t)\alpha - u^{-1}(t)\\ \implies \lambda_1(t)\alpha = u^{-1}(t)\\ \implies u(t) = \frac{1}{\alpha \lambda_1(t)}\) The optimal controller \(u^{*}(t)\) is thus independent of \(\lambda_2(t)\) and of the form \(u^{*}(t) = \frac{1}{\alpha \lambda_1(t)}\).
Expanding the adjoint system with the definition of the Hamiltonian, we get: \(\dot{\lambda}_1(t) = -\frac{\partial }{\partial x_1}\left(x_2(t)-\ln(u(t)) + \lambda_1(t)\left(\alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t)\right) + \lambda_2(t)\left(\delta(\epsilon x_2(t) - x_1(t))\right)\right)\\ =-\frac{\partial }{\partial x_1}\left(-\lambda_1(t)\beta x_1(t) + \lambda_1(t)\gamma x_2(t)x_1(t) - \lambda_2(t)\delta x_1(t)\right)\\ = \lambda_1(t)\beta + \lambda_2(t)\delta - \lambda_1(t)\gamma x_2(t)\\ \dot{\lambda}_2(t) = -\frac{\partial}{\partial x_2}\left(x_2(t)-\ln(u(t)) + \lambda_1(t)\left(\alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t)\right) + \lambda_2(t)\left(\delta(\epsilon x_2(t) - x_1(t))\right)\right)\\ =-\frac{\partial}{\partial x_2}\left(x_2(t) + \lambda_1(t)\gamma x_2(t)x_1(t) + \lambda_2(t)\delta \epsilon x_2(t)\right)\\ =-1-\lambda_1(t)\gamma x_1(t) - \lambda_2(t) \delta \epsilon\) Hence, the adjoint system is independent of \(u^{*}(t)\).
Substituting \(u(t)=u^{*}(t)=\frac{1}{\alpha \lambda_1(t)}\) in the state equations gives: \(\dot{x}_1(t) = f_1(x_1(t), x_2(t), u^{*}(t))=\alpha \frac{1}{\alpha \lambda_1(t)} - \beta x_1(t) + \gamma x_2(t)x_1(t)\\ =\frac{1}{\lambda_1(t)} - \beta x_1(t) + \gamma x_2(t)x_1(t)\\ \dot{x}_2(t) = f_2(x_1(t), x_2(t))=\delta(\epsilon x_2(t) - x_1(t))\) We thus have the following two-point boundary value problem that should be satisfied by any optimal trajectory \(x^{*}(\cdot)\) (Pontryagin [9]):
\(\dot{\lambda}_1(t)= \lambda_1(t)\beta + \lambda_2(t)\delta - \lambda_1(t)\gamma x_2(t) \quad \quad \text{subject to }\lambda_1(t_f)= 0\\ \dot{\lambda}_2(t) = -1-\lambda_1(t)\gamma x_1(t) - \lambda_2(t) \delta \epsilon \quad \quad \text{subject to }\lambda_2(t_f)= 0 \\ \dot{x}_1(t) =\frac{1}{\lambda_1(t)} - \beta x_1(t) + \gamma x_2(t)x_1(t) \quad \quad \text{subject to }x_1(0)= x_{1,real}(2000)\\ \dot{x}_2(t) =\delta(\epsilon x_2(t) - x_1(t)) \quad \quad \text{subject to }x_1(0)= x_{2,real}(2000)\) The system of differential equations above is non-linear and does not have an analytical solution in general. The system becomes linear if \(\gamma=0\), however. Further, if \(\gamma=0\), the adjoint system becomes decoupled from the state equations, allowing an analytical solution to be obtained.\newline
Assume \(\gamma=0\). Then: \(\dot{\lambda}_1(t)= \lambda_1(t)\beta + \lambda_2(t)\delta \quad\quad \text{subject to }\lambda_1(t_f)= 0\\ \dot{\lambda}_2(t) = -1 - \lambda_2(t) \delta \epsilon \quad\quad \text{subject to }\lambda_2(t_f)= 0 \\ \dot{x}_1(t) =\frac{1}{\lambda_1(t)} - \beta x_1(t) \quad\quad \text{subject to }x_1(0)= x_{1,real}(2000)\\ \dot{x}_2(t) =\delta(\epsilon x_2(t) - x_1(t)) \quad\quad \text{subject to }x_1(0)= x_{2,real}(2000)\) Since the equation for $\dot{\lambda}_2(t)$ is linear and independent of $\lambda_1(t)$ and the states, the analytical form is: \(\lambda_2(t) = e^{-\delta\epsilon (t-t_f)}\lambda_2(t_f) -\int_{t_f}^{t}e^{-\delta\epsilon (\tau-t_f)}d\tau\) Using the boundary condition \(\lambda_2(t_f)=0\), we get: \(\lambda_2(t) = e^{-\delta\epsilon (t-t_f)}\lambda_2(t_f) -\int_{t_f}^{t}e^{-\delta\epsilon (\tau-t_f)}d\tau\\ =\int_{t_f}^{t}-e^{-\delta\epsilon (\tau-t_f)}d\tau = \left[\frac{e^{-\delta\epsilon (\tau-t_f)}}{\delta\epsilon}\right]^{t}_{t_f}=\frac{e^{-\delta\epsilon(t-t_f)}-1}{\delta\epsilon}\) Plugging the analytical expression for \(\lambda_2(t)\) into the equation for \(\lambda_1(t)\), we get: \(\dot{\lambda}_1(t)= \lambda_1(t)\beta + \frac{e^{-\delta\epsilon(t-t_f)}-1}{\delta\epsilon}\delta \quad\quad \text{subject to }\lambda_1(t_f)= 0\) Using the boundary condition \(\lambda_1(t_f)= 0\) we obtain: \(\lambda_1(t) = e^{\beta(t-t_f)}\lambda_1(t_f) + \int_{t_f}^{t}\left(e^{\beta(\tau-t_f)}\frac{e^{-\delta\epsilon(\tau-t_f)}-1}{\epsilon}\right)d\tau\\ =\int_{t_f}^{t}\left(\frac{e^{\beta(\tau-t_f)-\delta\epsilon(\tau-t_f)}-e^{\beta(\tau-t_f)}}{\epsilon}\right)d\tau = \int_{t_f}^{t}\left(\frac{e^{\tau(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}-e^{\beta(\tau-t_f)}}{\epsilon}\right)d\tau\\ =\frac{1}{\epsilon}\left(\int_{t_f}^te^{\tau(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}d\tau - \int_{t_f}^te^{\beta(\tau-t_f)}d\tau\right) = \frac{1}{\epsilon}\left(\left[\frac{e^{\tau(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}}{\beta-\delta \epsilon}\right]_{t_f}^{t}-\left[\frac{e^{\beta(\tau-t_f)}}{\beta}\right]_{t_f}^{t}\right)\\ =\frac{1}{\epsilon}\left(\frac{e^{t(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}-1}{\beta-\delta \epsilon}- \frac{e^{\beta(t-t_f)}-1}{\beta}\right)\) The closed form expression for the optimal control then becomes: \(u^{*}(t)=\frac{1}{\alpha \lambda_1(t)} = \left(\frac{\alpha}{\epsilon}\left(\frac{e^{t(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}-1}{\beta-\delta \epsilon}- \frac{e^{\beta(t-t_f)}-1}{\beta}\right)\right)^{-1}\)
Numerical Results
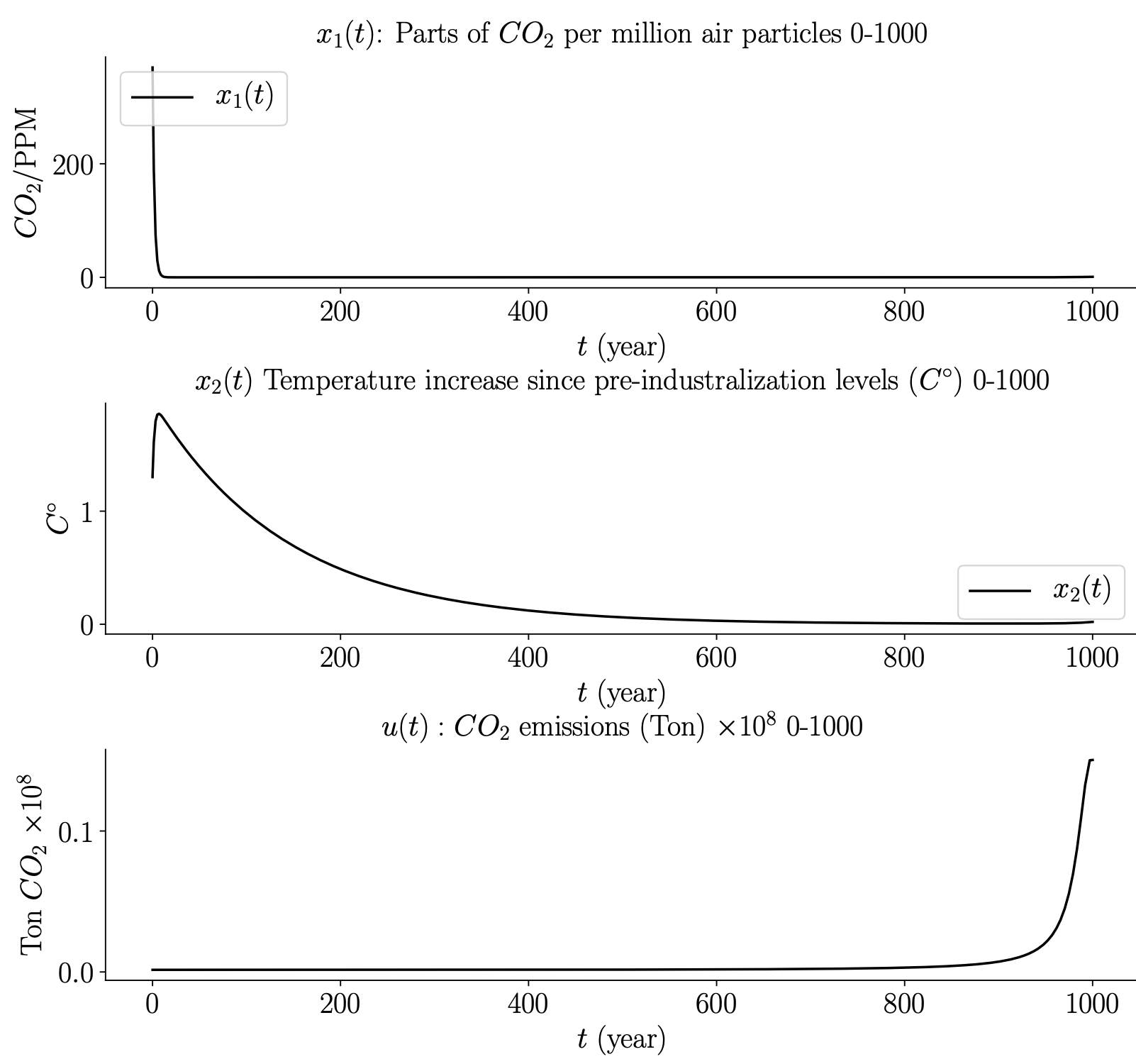
The numerical results from applying the control law:
\[u^{*}(t)=\frac{1}{\alpha \lambda_1(t)} = \left(\frac{\alpha}{\epsilon}\left(\frac{e^{t(\beta - \delta \epsilon) + t_f(\delta\epsilon - \beta)}-1}{\beta-\delta \epsilon}- \frac{e^{\beta(t-t_f)}-1}{\beta}\right)\right)^{-1}\]to the dynamics: \(\dot{x}(t) = f(x(t), u(t))= \begin{bmatrix} \alpha u(t) - \beta x_1(t) + \gamma x_2(t)x_1(t) \\ \delta(\epsilon x_2(t) - x_1(t)) \end{bmatrix}\)
with constants \(\alpha=0.9,\delta=-0.05,\beta=0.01,\gamma=0,\epsilon=0.14\) and \(t_f=1000\) are shown in the figure below. From the results in the figure we conclude that the optimal control is to reduce the \(CO_2\) emissions to a level close to zero for the coming \(800\) years and then to increase the emissions exponentially around year \(800\). This control law keeps the temperature increase safely below \(2\) degrees and quickly reduces the \(CO_2\) concentration in the atmosphere. That the optimal control is to first reduce the \(CO_2\) emissions and then to increase it is a result of the fixed time horizon \(t_f\). Since the time horizon is fixed, it is optimal to act myopically when close to the final time since any dynamical effects after the final time will not affect the cost. From this observation we conclude that to obtain more sensible results, an infinite horizon version of the optimal control problem should be considered.
Discussion
The current model and the optimal control solution seems not very realistic and only provides the obvious solution, to cut carbon emissions immediately to a minimum level. The benefits of such a cut in emissions are known but nevertheless are the changes not implemented on a global scale. Reasons for that could be a technical feasibility, were the entire world would collapse, if emissions were cut to zero immediately. Another more likely cause for that is a general disagreement on the costs of a cut in emissions as well as dynamics in the collective behaviour of humanity in terms of following policy’s which are not solely for the own short term benefit.
The current model is a simple zero-dimensional Energy Balance Model (EBM) which is based on the theory that the climate on earth has an equilibrium when the incoming energy from the sun that is absorbed by the earth is in balance with the dissipated energy that leaves the earth by radiation. Two important factors that have an impact on the dissipation are the greenhouse effect and the albedo effect. The greenhouse effect is governed by the emission of greenhouse gases as well as of the amount of clouds in the atmosphere. The albedo effect is mainly impacted by the amount of ice surfaces that reflect more energy back to space than surfaces with that are not coverd by ice. A second impact on the albedo effect is the amount of clouds as well.
Conclusion
In this project we have investigated climate engineering from an optimal control perspective. We have modeled the global climate as a nonlinear dynamical system, we have derived structural properties of the optimal control strategy using Pontryagin’s minimum principle, and we have computed numerical control values using nonlinear constrained optimization.
Our conclusion is that the global climate is too complex to be captured by a model with only a handful of parameters. However, using a simple model and applying optimal control provides valuable insight into how to design more advanced models and obtain more advanced control policies.
References
[1] Data Overview. Sept. 2022. URL: http://berkeleyearth.org/data/.
[2] Berkeley Earth. Climate change: Earth surface temperature data. May 2017. URL: https://www.kaggle.com/datasets/berkeleyearth/climate-change-earth-surface-temperature-data.
[3] Paul N. Edwards. A Vast Machine: Computer Models, Climate Data, and the Politics of Global Warming. The MIT Press, 2010. ISBN: 9780262518635. URL: http://www.jstor.org/stable/j.ctt5hhds1 (visited on 10/04/2022).
[4] Paul N. Edwards. “History of climate modeling”. In: Wiley Interdisciplinary Reviews: Climate Change 2 (2011).
[5] Gary Erickson. Optimal Control of Global Warming. 2012.
[6] Donald R. Jones, Matthias Schonlau, and William J. Welch. “Efficient Global Optimization of Expensive Black-Box Functions”. In: J. of Global Optimization 13.4 (Dec. 1998), pp. 455–492. ISSN: 0925-5001. DOI: 10.1023/A:1008306431147. URL: https://doi.org/10.1023/A:1008306431147.
[7] United Nations. Paris Agreement. 2015.
[8] William D. Nordhaus. “To Slow or Not to Slow: The Economics of The Greenhouse Effect”. In: The Economic Journal 101.407 (1991), pp. 920–937. ISSN: 00130133, 14680297. URL: http://www.jstor. org/stable/2233864 (visited on 10/06/2022).
[9] L.S. Pontrjagin. The Mathematical Theory of Optimal Processes. Interscience Publ., 1962. URL: https: //books.google.se/books?id=jzJPAQAAIAAJ.
[10] Regeringskansliet. En samlad politik fo ̈r klimatet. 2020.
[11] The Royal Society. Climate change: a summary of the science. 2010.
[12] Gustav Strandberg. Säkerhet och osäkerhet i klimatscenarierna. 2020.